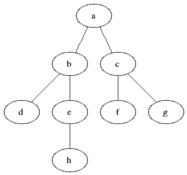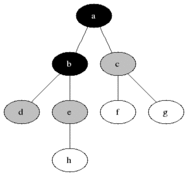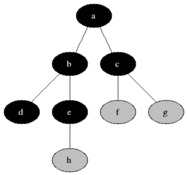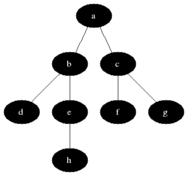
그래프 탐색 알고리즘은 노드(정점)과 엣지(간선)으로 구성된 그래프 구조에서 데이터를 탐색하거나 최적화하는 기법을 의미한다. 그래프는 데이터 간의 관계를 효율적으로 표현하는 자료구조로, 다양한 알고리즘을 통해 원하는 정보를 찾거나 경로를 계산할 수 있다.

Traversal Search는 그래프의 모든 노드를 순회하는 기법을 의미하며, 이 탐색 방법은 그래프에서 원하는 데이터를 찾거나 특정 경로를 탐색할 때 유용하게 활용된다.

  • DFS(Depth First Search): 깊이 우선 탐색
  • BFS(Breadth First Search): 너비 우선 탐색

DFS

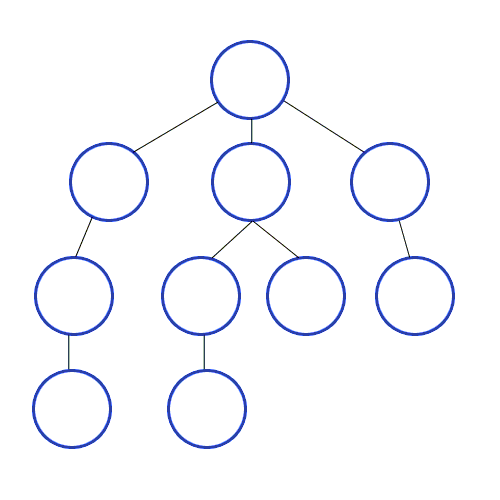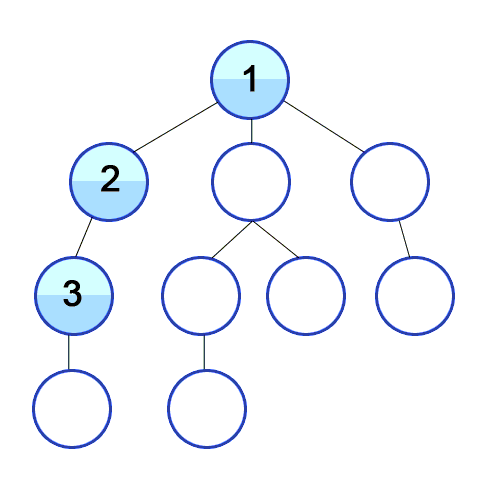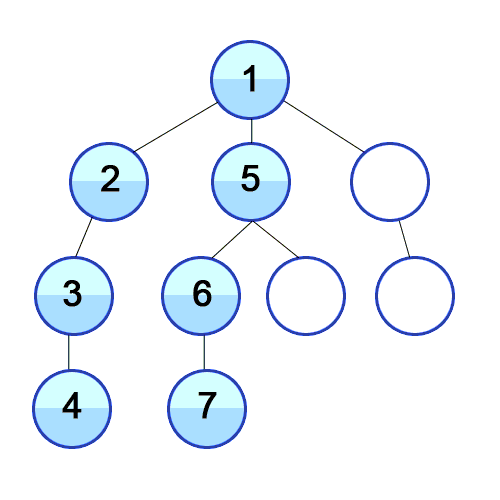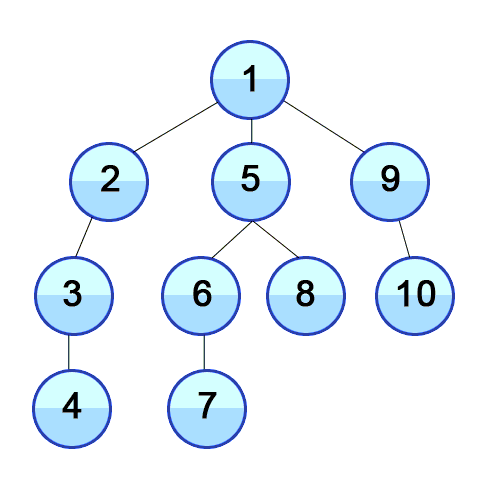
DFS(Depth First Search)는 한 노드에서 시작하여 가능한 한 깊이 내려간 후, 더 이상 탐색할 곳이 없으면 되돌아가면서 방문하는 방식이다. 이 탐색 방식은 Stack 자료구조 또는 재귀 호출을 활용하여 구현할 수 있다.

def dfs(graph, node, visited):
    if node not in visited:
        visited.append(node)
        for neighbor in graph[node]:
            dfs(graph, neighbor, visited)

if __name__ == "__main__":
    graph = {
        1: [2, 5, 9],
        2: [1, 3],
        3: [2, 4],
        4: [3],
        5: [1, 6, 8],
        6: [5, 7],
        7: [6],
        8: [5],
        9: [1, 10],
        10: [9]
    }
    visited = []

    dfs(graph, 1, visited)
    print("Traversal elements:", visited)

Traversal elements: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

BFS

BFS(Breadth First Search)는 시작 노드에서 가까운 노드부터 차례대로 방문하는 방식이다. 이 탐색 방식은 Queue 자료구조를 활용하여 구현되며, 방문할 노드를 순서대로 저장하고 꺼내면서 탐색을 진행한다.

from collections import deque

def bfs(graph, start):
    visited = []
    queue = deque([start])

    while queue:
        node = queue.popleft()
        if node not in visited:
            visited.append(node)
            queue.extend(graph[node])
    
    return visited


if __name__ == "__main__":
    graph = {
        "A": ["B", "C"],
        "B": ["A", "D", "E"],
        "C": ["A", "F", "G"],
        "D": ["B"],
        "E": ["B", "H"],
        "F": ["C"],
        "G": ["C"],
        "H": ["E"]
    }

    visited = bfs(graph, "A", visited)
    print("Traversal elements:", visited)

Traversal elements: ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H']

그래프에서 한 노드에서 다른 노드까지의 최단 경로를 찾는 알고리즘을 의미한다. 이 탐색 방법은 그래프의 가중치와 구조에 따라 다양한 방식으로 구현될 수 있으며, 특정 요구 사항에 맞는 최적의 알고리즘이 선택된다.

  • Dijkstra: 가중 그래프에서 최단 경로 탐색
  • Bellman-Ford: 음수 가중치를 포함한 그래프에서 최단 경로 탐색
  • Floyd-Warshall: 모든 노드 간 최단 경로 탐색

Dijkstra

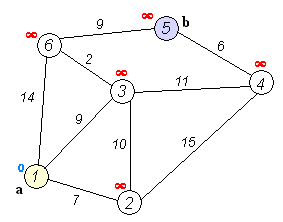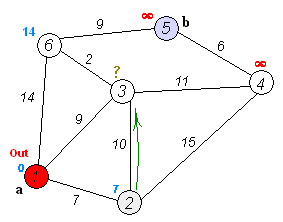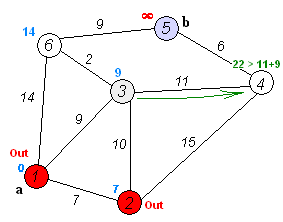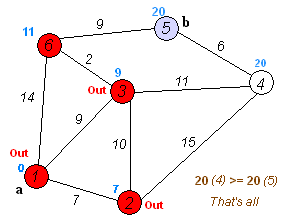
Dijkstra 알고리즘은 가중 그래프에서 최단 경로를 찾는 대표적인 알고리즘으로, Priority Queue 를 활용하여 최단 경로를 점진적으로 탐색한다.

import heapq

def dijkstra(graph, start):
    distances = {node: float("inf") for node in graph}
    distances[start] = 0
    queue = [(0, start)]

    while queue:
        current_distance, current_node = heapq.heappop(queue)

        if distances[current_node] < current_distance:
            continue

        for neighbor, weight in graph[current_node].items():
            distance = current_distance + weight

            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(queue, (distance, neighbor))

    return distances

if __name__ == "__main__":
    graph = {
        1: {2: 7, 3: 9, 6: 14},
        2: {1: 7, 3: 10, 4: 15},
        3: {1: 9, 2: 10, 4: 11, 6: 2},
        4: {2: 15, 3: 11, 5: 6},
        5: {4: 6, 6: 9},
        6: {1: 14, 3: 2, 5: 9}
    }

    data = dijkstra(graph, 1)
    distance_data = [f"{key}: {value}" for key, value in data.items()]
    print("Shortest path from node 1:")
    print('\n'.join(distance_data))

Shortest path from node 1:
1: 0
2: 7
3: 9
4: 20
5: 20
6: 11

Ranking Search는 그래프 기반의 데이터에서 개별 노드의 중요도를 평가하는 검색 기법을 의미한다. 단순한 탐색이나 최단 경로 탐색과 달리, 각 노드의 중요도나 순위를 결정하는 데 초점을 맞춘다.

  • PageRank: 웹페이지 중요도 평가
  • Eigenvector Centrality: 연결 구조를 기반으로 영향력 분석
  • Betweenness Centrality: 최단 경로에서 중개 역할을 하는 노드 분석

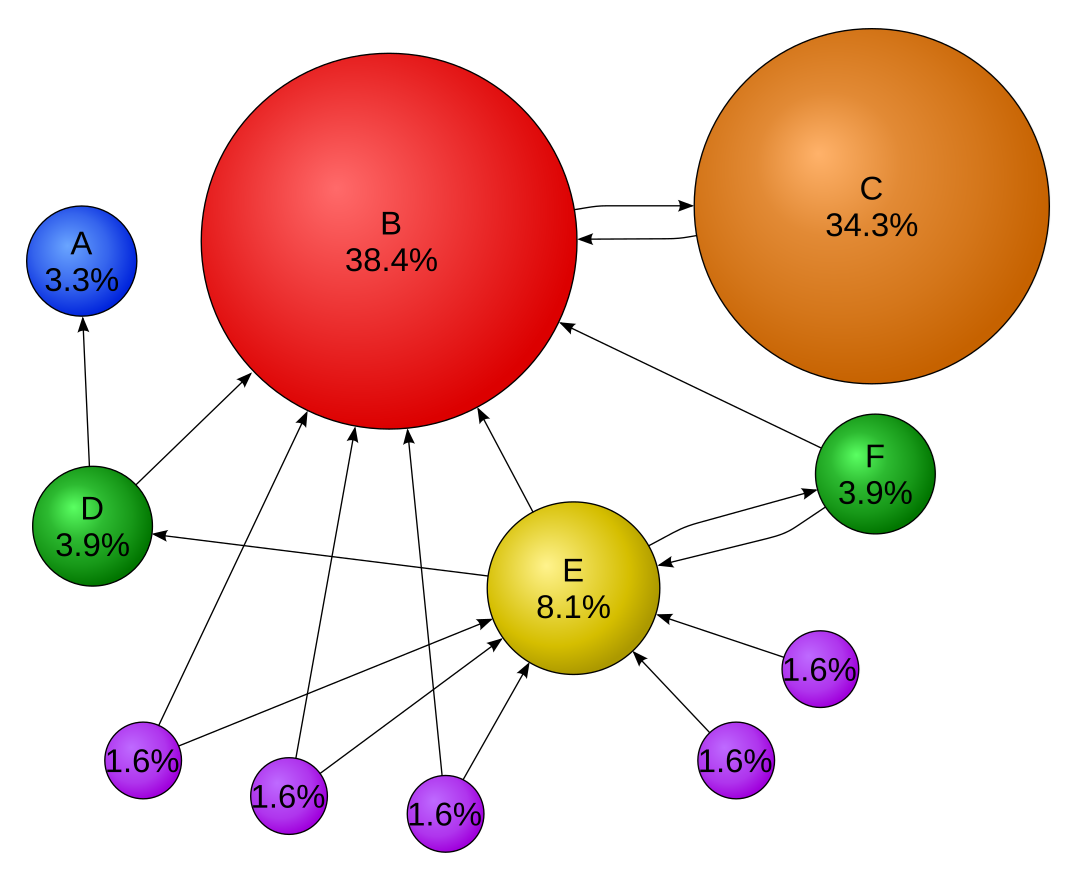
PageRank

PageRank 알고리즘은 구글 검색 엔진의 핵심 알고리즘으로, 웹페이지의 중요도를 평가하는 기법이다. 웹페이지 간의 링크 구조를 분석하여, 많은 링크를 받거나, 중요한 페이지로부터 링크를 받은 페이지일수록 높은 점수를 얻는다.

import numpy as np

def page_rank(graph, alpha=0.85, max_iter=100, tol=1.0e-6):
    nodes = list(graph.keys())
    N = len(nodes)
    M = np.zeros((N, N))

    for i, node in enumerate(nodes):
        if graph[node]:
            for neighbor in graph[node]:
                j = nodes.index(neighbor)
                M[j, i] = 1 / len(graph[node])

    rank = np.ones(N) / N
    for _ in range(max_iter):
        new_rank = alpha * np.dot(M, rank) + (1 - alpha) / N
        if np.linalg.norm(new_rank - rank) < tol:
            break
        rank = new_rank

    return {nodes[i]: rank[i] for i in range(N)}

if __name__ == "__main__":
    graph = {
        "A": [],
        "B": ["C"],
        "C": ["B"],
        "D": ["A", "B"],
        "E": ["B", "D", "F"],
        "F": ["B", "E"],
        "G": ["B", "E"],
        "H": ["B", "E"],
        "I": ["B", "E"],
        "J": ["E"],
        "K": ["E"],
    }

    data = page_rank(graph)
    percentage_data = [f"{key}: {value * 100:.2f}%" for key, value in data.items()]
    print("Ranking value:")
    print('\n'.join(percentage_data))

Ranking value:
A: 2.76%
B: 32.42%
C: 28.92%
D: 3.30%
E: 6.82%
F: 3.30%
G: 1.36%
H: 1.36%
I: 1.36%
J: 1.36%
K: 1.36%

References